tug/doc/ADI_scheme.org

Adi Scheme

• Input
• Internals
• Calculation for $\frac{1}{2}$ timestep
  • Symbolic addressing of grid cells
  • Filling of matrix $A$
    • Rules
      • Ghost nodes
      • Inlet
  • Filling of vector $b$
    • Rules
      • Ghost nodes
    • Inlet

Input

• c $\rightarrow c$

  • containing current concentrations at each grid cell for species
  • size: $N \times M$
  • row-major

• alpha $\rightarrow \alpha$

  • diffusion coefficient for both directions (x and y)
  • size: $N \times M$
  • row-major

• boundary_condition $\rightarrow bc$

  • Defines closed or constant boundary condition for each grid cell
  • size: $N \times M$
  • row-major

Internals

• A_matrix $\rightarrow A$

  • coefficient matrix for linear equation system implemented as sparse matrix
  • size: $((N+2)\cdot M) \times ((N+2)\cdot M)$ (including ghost zones in x direction)
  • column-major (not relevant)

• b_vector $\rightarrow b$

  • right hand side of the linear equation system
  • size: $(N+2) \cdot M$
  • column-major (not relevant)

• x_vector $\rightarrow x$

  • solutions of the linear equation system
  • size: $(N+2) \cdot M$
  • column-major (not relevant)

Calculation for $\frac{1}{2}$ timestep

Symbolic addressing of grid cells

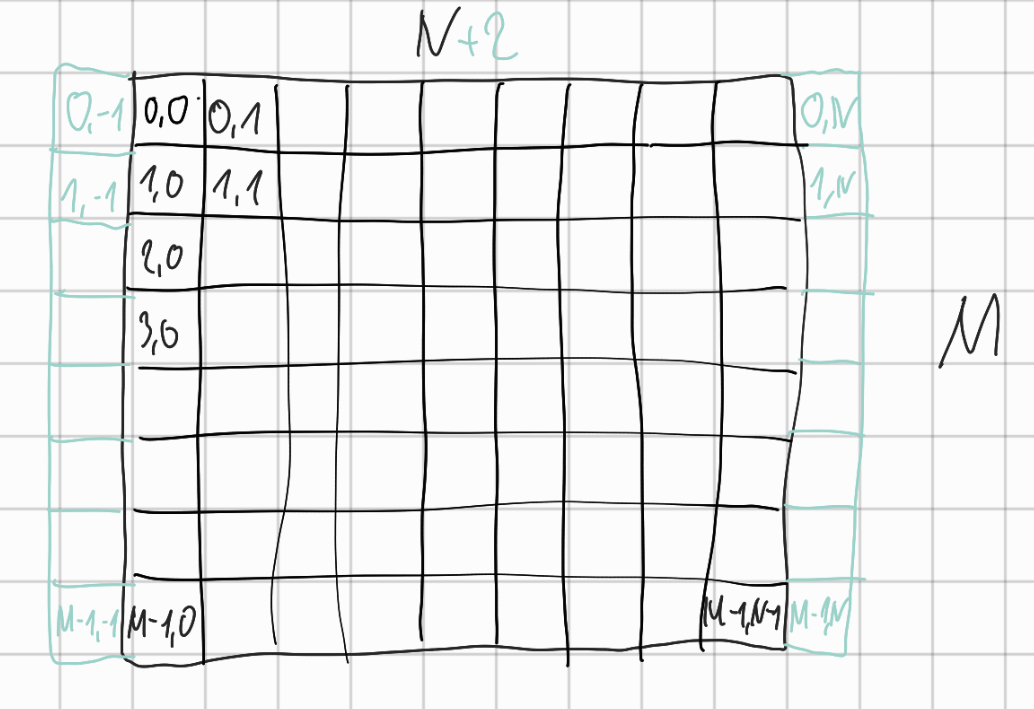
Filling of matrix $A$

• row-wise iterating with $i$ over c and \alpha matrix respectively
• addressing each element of a row with $j$

• matrix $A$ also containing $+2$ ghost nodes for each row of input matrix $\alpha$

  • $\rightarrow offset = N+2$
  • addressing each object $(i,j)$ in matrix $A$ with $(offset \cdot i + j, offset \cdot i + j)$

Rules

$s_x(i,j) = \frac{\alpha(i,j)*\frac{t}{2}}{\Delta x^2}$ where $x$ defining the domain size in x direction.

For the sake of simplicity we assume that each row of the $A$ matrix is addressed correctly with the given offset.

Ghost nodes

$A(i,-1) = 1$

$A(i,N) = 1$

Inlet

$A(i,j) = \begin{cases} 1 & \text{if } bc(i,j) = \text{constant} \\ -1-2*s_x(i,j) & \text{else} \end{cases}$

$A(i,j\pm 1) = \begin{cases} 0 & \text{if } bc(i,j) = \text{constant} \\ s_x(i,j) & \text{else} \end{cases}$

Filling of vector $b$

• each elements assign a concrete value to the according value of the row of matrix $A$

• Adressing would look like this: $(i,j) = b(i \cdot (N+2) + j)$

  • $\rightarrow$ for simplicity we will write $b(i,j)$

Rules

Ghost nodes

$b(i,-1) = \begin{cases} 0 & \text{if } bc(i,0) = \text{constant} \\ c(i,0) & \text{else} \end{cases}$

$b(i,N) = \begin{cases} 0 & \text{if } bc(i,N-1) = \text{constant} \\ c(i,N-1) & \text{else} \end{cases}$

Inlet

$p(i,j) = \alpha(i,j)\frac{c(i-1,j) - 2\cdot c(i,j) + c(i+1,j)}{\Delta x^2}$¹

$b(i,j) = \begin{cases} bc(i,j).\text{value} & \text{if } bc(i,N-1) = \text{constant} \\ -c(i,j)-p(i,j) & \text{else} \end{cases}$

---

¹

$p$ is called t0_c inside code